Sabit Göreli Fiyatlı GSYH Alt Bileşenlerini Nasıl Türetebiliriz?

Bir önceki “Reel GSYH Büyümesine Alt Bileşenlerin Katkısının Hesaplanması: 2022 ve 2023 Yılları” başlıklı yazımızda sabit fiyatlı seriler üzerinden reel GSYH büyümesine katkının nasıl hesaplandığını 1 numaralı denklem ile göstermiştik:

1. (t dönemindeki Reel Tüketim Miktarı – t-1 dönemindeki Reel Tüketim Miktarı) / (t-1 dönemindeki Reel GSYH Miktarı)

Zincirlenmiş hacim endeksi serileri üzerinden reel GSYH büyümesine alt bileşenlerin katkılarının nasıl hesaplandığını ise 2 numaralı denklem ile göstermiştik.

2. [(t dönemindeki Reel Tüketim Miktarı – t-1 dönemindeki Reel Tüketim Miktarı) / (t-1 dönemindeki Reel GSYH Miktarı)] * (t-1 dönemindeki Tüketim Deflatörü / t-1 dönemindeki GSYH Deflatörü)

Dikkatli bakılırsa 2 numaralı denklem, 1 numaralı denklem ile bir önceki yılın göreli fiyatının (Tüketim Deflatörü/GSYH Deflatörü) çarpımıdır.

Sabit fiyatlı bir seride bir baz yıl seçilir ve o fiyat sabit kabul edilerek reel GSYH ve alt bileşenler oluşturulur. Yani, sabit fiyatlı bir seride baz yılındaki göreli fiyat, reel GSYH ve alt bileşenler oluşturulmasında yıllarca kullanılır. Bu yüzden 2 numaralı denklemin sarı vurgulu alanı aslında 1 numaralı denklemde de var ancak sabit fiyatlı bir seride denklemin bu kısmının değeri hep 1 değerini (1/1=1) alır.

Bir örnekle sabit yıllı reel GSYH’nin mantığını açıklayalım. Sabit yılımız 2015 olsun ve biz 2023 yılı reel GSYH değerini hesaplamak istiyoruz. Fiyatlar 2015 yılındaki gibi olsaydı 2023 yılı için hesapladığımız nominal GSYH’nin değeri ne kadarlık bir reel GSYH değerine eşit olurdu?

Zincirlenmiş hacim endeksinde ise, şu soru sorulur: Fiyatlar bir önceki yıldaki gibi olsaydı 2023 yılı için hesapladığımız nominal GSYH’nin değeri ne kadarlık bir reel GSYH değerine eşit olurdu? Burada nominal GSYH’yi reel GSYH’ye dönüştürmek için her zaman bir önceki yılı baz alıyoruz. Bu yüzden hep baz yılımız değişiyor. 2022 yılı reel GSYH hesaplamasında baz yılı 2021 iken 2023 yılı reel GSYH hesaplamasında baz yılımız 2022 oldu. Baz yılımız her yıl değiştiği için alt bileşenler ile reel GSYH arasındaki göreli fiyatta her yıl değişiyor. Zincirlenmiş hacim endeksinde büyümeye katkıları hesaplarken baz yılının her yıl değişmesi sebebiyle ortaya çıkan göreli fiyat etkisini ortadan kaldırıyoruz.

2009 Yılı Sonrası İçin Sabit Göreli Fiyatlı Reel GSYH Alt Bileşenleri Serilerinin Türetilmesi

Eğer biz göreli fiyat etkisini ortadan kaldırarak büyümeye katkı hesabı yapabiliyorsak, göreli fiyat etkisinden arındırılmış GSYH’nin alt bileşenlerini türetebiliriz. Bu seri toplamsallık sorunu bulunmayan bir seri olur. Bu serinin göreli fiyatları her yıl için 1 olur. TÜİK GSYH serilerinde 2009 yılı baz yılı olduğu için serimi 2009 yılına göre türetmeliyiz.

3. 2009 yılı Tüketim Miktarı + [(2010 yılı Reel GSYH – 2009 Yılı Reel GSYH)*(2010 Yılı Tüketimin Büyümeye Katkısı / 2010 Yılı Reel GSYH’nin Büyümesi)] = Sabit Göreli Fiyatlı 2010 Yılı Tüketim Miktarı

2010 yılı sabit göreli fiyatlı Tüketim Miktarı verisini oluşturduktan sonra 2011 yılı sabit göreli fiyatlı Tüketim Miktarı serisini oluşturmalıyım. 2011 ve sonrası yıllar için denklemimizdeki küçük farklılık aşağıda vurgulanmıştır.

4. Sabit Göreli Fiyatlı 2010 yılı Tüketim Miktarı + [(2011 yılı Reel GSYH – 2010 Yılı Reel GSYH)*(2011 Yılı Tüketimin Büyümeye Katkısı / 2011 Yılı Reel GSYH’nin Büyümesi)] = Sabit Göreli Fiyatlı 2011 Yılı Tüketim Miktarı

Bunu her yıl için yaptığımda 2009-2023 dönemi için sabit göreli fiyatlı (2009 yılındaki göreli fiyatlara göre sabitlenmiş) reel GSYH alt bileşenler serisini oluşturabilirim.

Yukarıdaki 3 numaralı denklemi bir kaç matematiksel işlemle şu hale getirebiliriz:

2009 yılı Tüketim Miktarı + [(2010 yılı Tüketim Miktarı – 2009 Yılı Tüketim Miktarı)*(2009 Yılı Tüketim Deflatörü / 2009 Yılı Reel GSYH Deflatörü] = Sabit Göreli Fiyatlı 2010 Yılı Tüketim Miktarı

2009 yılını baz alarak 2010-2023 dönemini için reel GSYH alt bileşenler serisini türetmiş olduk. 2009 öncesi seriyi nasıl türeteceğiz?

2009 Yılı Öncesi İçin Sabit Göreli Fiyatlı Reel GSYH Alt Bileşenleri Serilerinin Türetilmesi

3 ve 4 numaralı denklemlerde küçük bir değişiklik yapacağız ve 5 ile 6 numaralı denklemleri elde edeceğiz: Çünkü artık 2009 yılı sonrasını değil, 2009 yılı öncesini türetmek istiyoruz.

5. 2009 yılı Tüketim Miktarı – [(2009 yılı Reel GSYH – 2008 Yılı Reel GSYH)*(2009 Yılı Tüketimin Büyümeye Katkısı / 2009 Yılı Reel GSYH’nin Büyümesi)] = Sabit Göreli Fiyatlı 2008 Yılı Tüketim Miktarı

6. Sabit Göreli Fiyatlı 2008 yılı Tüketim Miktarı – [(2008 yılı Reel GSYH – 2007 Yılı Reel GSYH)*(2008 Yılı Tüketimin Büyümeye Katkısı / 2008 Yılı Reel GSYH’nin Büyümesi)] = Sabit Göreli Fiyatlı 2007 Yılı Tüketim Miktarı

Türetilmiş Veriler 2021-2023

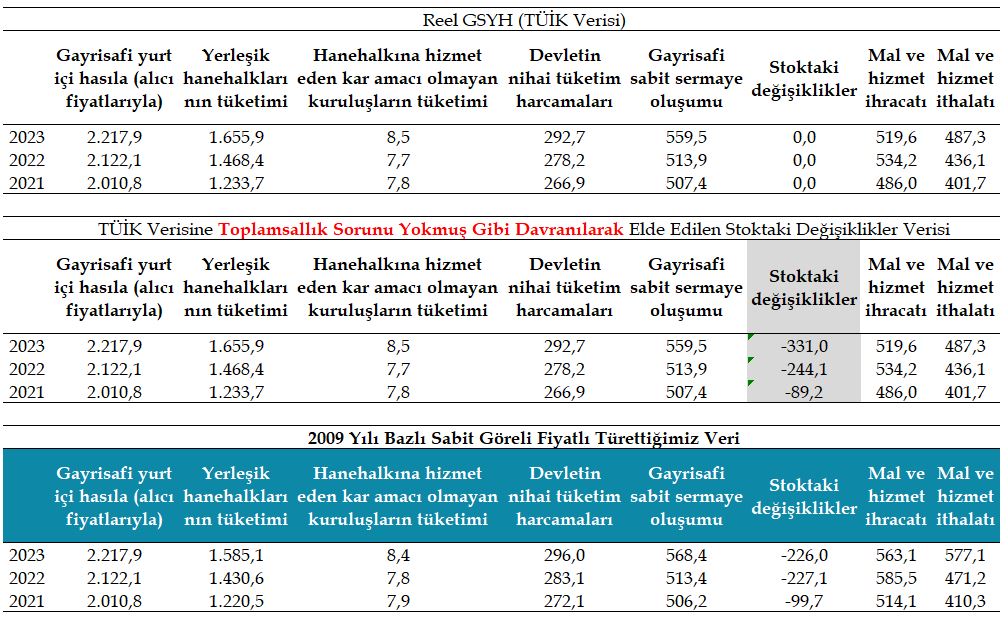
Aşağıdaki tabloda ilk grup 2021-2023 verisi TÜİK’ten elde edilmiş ham veridir. Dikkat edilirse stoktaki değişklikler kaleminde veri yoktur. Bunun nedeni daha öncede ifade ettiğimiz üzere, zincirlenmiş hacim endeksinde toplamsallık sorunu bulunmasıdır. Yani, alt bileşenlerin toplamı üst bileşenlere eşit olamaz.

Toplamsallık soruna rağmen, TÜİK’ten elde edilen verilere toplamsallık sorunu yokmuş gibi davranılarak TÜİK’in bizlere sunmadığı veriyi araştırmacıların kendilerinin doldurduğu durum, ikinci grup 2021-2023 verisidir. Bu veriye bakılırsa stoktaki değişiklikler kalemi 2023 için -331 milyar TL’dir: Tarih sütununun 1. sütun olarak kabul ettiğimizde, 3.,4.,5.,6.,8. sütunu toplayıp 9. sütunu çıkartıldığında yurt içi harcamalara ulaşılır. Yurt içi harcamalar’dan GSYH’yi çıkarıldığında (2. sütun), stoktaki değişikliklere ulaşılır (7. sütun).

Toplamsallık soruna rağmen, TÜİK’ten elde edilen verilere toplamsallık sorunu yokmuş gibi davranılarak büyümeye katkıyı da yukarıdaki 1. numaralı denklem aracılığıyla hesaplanıyor.

Biz ise, toplamsallık sorununun farkında olarak, önce bu sorundan kurtularak büyümeye katkıları hesapladık. Bu şekilde göreli fiyatlardaki değişiklik sorununu ortadan kaldırdık: 1 numaralı denklemi bir önceki yılın göreli fiyatları ile çarptık. Yani 2 numaralı denklemi kullandık.

2009 yılı baz yılı olduğu için nominal GSYH verileri reel GSYH verilerine eşit olur. Dolayısıyla 2009 yılındaki stoktaki değişiklikler kalemini biliyoruz. Büyümeye katkıları hesapladıktan sonra 2009 yılını baz alarak (yani tüm göreli fiyatları 2009 yılına eşitleyerek, baz yılı olduğu için teknik olarak 1’e eşitlemiş olduk) sabit göreli fiyatlı reel GSYH alt bileşenlerini oluşturduk. Bizim göreli fiyatlarımız artık değişken olmadığı için, türetmiş olduğumuz reel GSYH alt bileşenlerimiz toplanabilir hale geldi.

3. grup 2021-2023 reel GSYH verileri ile TÜİK’ten elde edilen (1. grup ) reel GSYH verilerine dikkatli bakılırsa tek değişmeyen veri reel GSYH serisidir, diğer tüm veriler değişmiştir (tüketim, yatırım…).

Sabit göreli fiyatlı verilerimize göre, stoktaki değişiklikler kalemi -226 milyar TL’dir. Stoktaki değişiklikler kaleminin negatif değer alması ekonomideki yurt içinde üretilen mal ve hizmetlere yönelik toplam harcamaların üretimi aştığını ifade eder. Böyle bir durumda üreticiler, harcamaları karşılayabilmek çin geçmiş yıllardaki stoklarını kullanmış olurlar. Stoktaki değişiklikler kaleminin pozitif değer alması ise ekonomideki yurt içinde üretilen mal ve hizmetlere yönelik harcamaların üretimin altında kaldığını ifade eder. Böyle bir durumda üreticiler ürettikleri ürünlerin tamamını satamadığından, ekonomide bir stok artışı olur.

TÜİK’in ham verisinden hareketle stok hesabı yapamayacağımızı daha önce vurgulamıştık. Ancak sabit göreli fiyatlı ürettiğimiz serilere göre Türkiye ekonomisi 2023 yılında 226 milyar TL, 2022 yılında 227 milyar TL ve 2021 yılında ise 99,7 milyar TL’lik harcamaları geçmiş yıllarda yaptığı stoklardan karşılamıştır. Firmalar Son 3 yılda yaklaşık reel olarak 550 milyar TL’lik stoktan satış yapmıştır. Buradaki temel soru şu: Bu kadar stok ne zaman üretildi? 550 milyar TL 2023 yılı reel GSYH’sinin (2,22 Trilyon TL) yaklaşık %25’dir. Ayrıca stok mallara ilişkin bir kavramdır, hizmetler stoklanamaz.

Ayrıca nominal GSYH rakamalarına göre, 2022 yılında Türkiye Ekonomisi 882 milyar stok artışı yaşarken, 2023 yılında 779 milyar TL stoktan satış yapmıştır. 2021 yılında ise Türkiye Ekonomisi’nde 235 milyar TL stok artışı yaşanmıştır.

GSYH hesaplamarında esas olan üretim yöntemi ile GSYH’dir.

E-Yani?

Bu konuyla ilgili ilk yazımızda reel GSYH Büyümesine alt bileşenlerin büyümeye katkısını nasıl hesaplayacağımızı tartışmıştık. Büyümeye katkıları nasıl hesaplandığını hem teknik hem de mantıksal açıdan öğrendikten sonra göreli fiyatları sabitleyerek yeni bir reel GSYH serisi oluşturabileceğimizi farkettik ve oluşturduk.

Bu yeni oluşturduğumuz sabit göreli fiyatlı reel GSYH verilerinin önemi ne? Bu yeni verilerin önemi, bir veriyi GSYH’ye oranlayacağımızda ortaya çıkmaktadır. Eğer TÜİK’in verisini kullanarak göreli fiyat etkisi olacağı için bir sektörün (reel imalat sanayi katma değerinin) ya da bir harcama grubunun ( reel tüketimin) reel GSYH’ye oranını doğru ölçümleyemeyiz.

Eğer bir alt bileşenen reel GSYH oranına bakacaksak, sabit göreli fiyatlı reel GSYH veri setimizi kullanmalıyız. Örneğin, reel imalat sanayi katma değerinin (ya da yatırımların, tüketimin) reel GSYH’ye oranı…

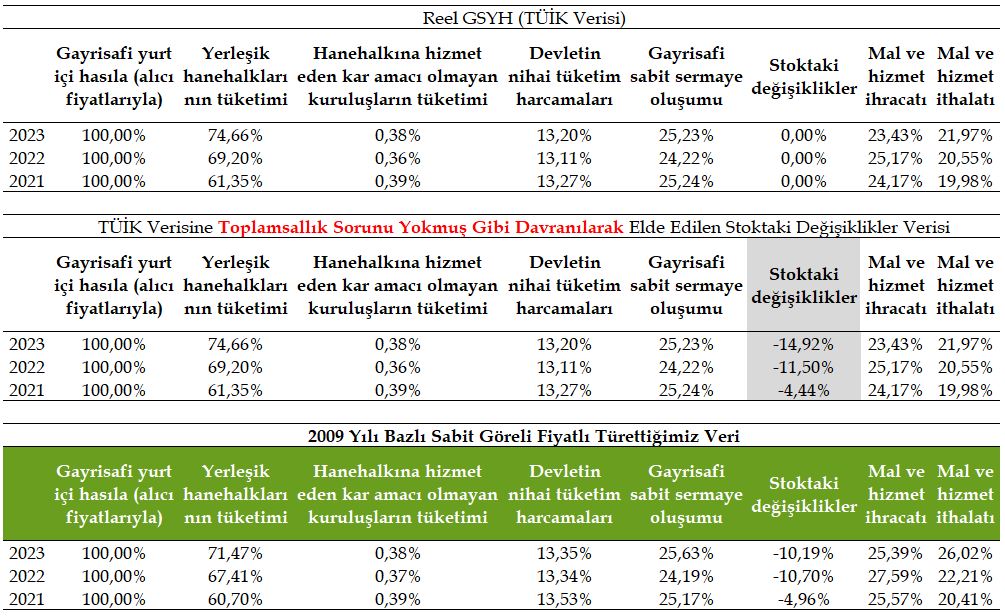
Aşağıdaki tabloda alt bileşenlerin reel GSYH’ye oranları sunulmuştur. TÜİK’in verisi dikkate alındığında (toplamsallık sorunu sebebiyle aslında TÜİK’in verisi ile böyle bir işlem yapamayacağımızı unutmadan) 2023 yılında tüketimin GSYH içindeki payı %74,66 iken, türetmiş olduğumuz sabit göreli fiyatlı veriler üzerinden tüketimin GSYH içindeki payı %71,47’dir. 2023 yılında çarpıcı farklılık ithalatın GSYH’ye oranında ortaya çıkıyor. Aradaki farklar “teknik açıdan” göreli fiyat etkisinden kaynaklanmaktadır.

Eğer bir alt bileşenin kendi büyümesini kullanacaksak TÜİK’in verisini kullanmalıyız. Örneğin, tüketimin yıllık büyümesi, reel imalat sanayi katma değeri büyümesi…

TÜİK verisi üzerinden büyümeye katkıları 2 numaralı denklemle hesaplıyoruz. Ancak elimizde sabit göreli fiyatlı reel GSYH verileri varsa, bu veriye 1 numaralı denklemi uygulayarak da aynı sonuçları elde ederiz. Çünkü, 2 numaralı denklemin amacı değişken göreli fiyatları sabit hale getirmektir, ancak bizim verilerimiz daha önceden türettiğimiz sabit göreli fiyatlı seriyse tekrardan göreli fiyat etkisinden arındırma işlemine ihtiyacımız yok. Ancak 2 numaralı denklemi sabit göreli fiyatlı bir seriye uygulamak da hatalı değildir, çünkü sabit göreli fiyatlı serimizde sabit göreli fiyat daima 1’dir. Bu yüzden sonucumuzu değiştirmez.