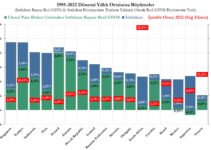
YILLARA GÖRE DOLAR BAZINDA GSYH | TL BAZINDA GSYH
TÜİK verilerinde ulusal para birimi cinsinden Gayrisafi Yurt İçi Hasıla (GSYH) verilerinde baz yılı değişikliği sebebiyle bu yıllarda verilerde kırılma vardır. Bu kırılmaları düzeltip TÜİK’in günümüzde yayınladığı verilerle uyumlu hale getirmeliyiz.
“TÜİK 100 Yılın Göstergeleri” excellerinden 19_Ulusal Hesaplar dosyasını açıp 3. ve 4 sayfadaki Nominal GSYH, Reel GSYH ve Büyüme Oranlarını birleştirdiğimizde 1923-2022 yılına ilişkin GSYH serisi elde ederiz. Ancak bu oluşturduğumuz tüm seri bugün kullandığımız gibi 2009 Bazlı Zincirlenmiş Hacim Endeksi verisi değildir: “1923-1947 yılları arası 1948=100 bazlı, 1948-1967 yılları 1968=100 bazlı, 1968-1997 yılları için 1987=100 bazlı GSMH serisi kullanılmaktadır.”
Oluşturduğumuz verileri incelersek 1948, 1968 ve 1998 yılı verileri ile bunların bir önceki yıllarını kıyaslarsak bir anormallik olduğunu farkederiz. Bunu düzelteceğiz.
İşlemleri takip etmek ve sonuçlar için aşağıdaki Excel dosyasını indiriniz.
Yıllara Göre 2009 Fiyatlarıyla Reel GSYH | 1923-2023
1 | İlk olarak Reel GSYH serisini bugün olduğu gibi 2009 ile uyumlu hale getireceğiz. Bunun için 1948, 1968 ve 1998 yılı büyüme oranlarına ihtiyacımız var. Çünkü bu 3 yıla ait büyüme oranı TÜİK’ten oluşturduğumuz seride bulunmamaktadır.
2009 fiyatlarıyla 2023 yılı Reel GSYH’nin değeri = 2022 Yılı Reel GSYH*[1+2023 Yılı Büyüme Oranı]
Benim amacım, tüm veriyi TÜİK’in cari dönemde açıklamış olduğu veriye göre uyumlu hale getirmek olduğu için, geçmiş verileri düzeltmeliyim. Böyle bir durumda yukarıdaki işlemi tersine yaparak geçmiş tarihe gitmeliyim.
2009 fiyatlarıyla 2022 yılı Reel GSYH’nin değeri = 2023 Yılı Reel GSYH/ [1+2023 Yılı Büyüme Oranı]
2009 fiyatlarıyla 2021 yılı Reel GSYH’nin değeri = 2022 Yılı Reel GSYH/ [1+2022 Yılı Büyüme Oranı]
.
.
.
2009 fiyatlarıyla 1923 yılı Reel GSYH’nin değeri = 1924 Yılı Reel GSYH/ [1+1924 Yılı Büyüme Oranı]
Bu işlemler ile 1923-2023 dönemi reel GSYH serisini 2009 fiyatlarıyla türetmiş oldum.
Yıllara Göre 2009 Bazlı GSYH Deflatör Endeksi | 1923-2023 | TÜİK İle Uyumlu
2 | Reel GSYH serisini türettiğime göre, deflatörü de türetirsem nominal GSYH serisine ulaşabilirim. Neyseki TÜİK 1948,1968 ve 1998 yılına ilişkin deflatör üzerinden enflasyon oranlarını 16_Fİyatlar ve Endeksler exelinde sunmuştur. Bu verileri kullanarak 2009=1 olacak şekilde 1923-1997 dönemini türeteceğiz.
2023 yılı Deflatör Endeksi = 2022 Yılı Deflatör Endeksi*[1+2023 Yılı Deflatör Üzerinden Enflasyon Oranı]
Benim amacım, tüm veriyi TÜİK’in cari dönemde açıklamış olduğu defaltöre göre uyumlu hale getirmek olduğu için, geçmiş verileri düzeltmeliyim. Böyle bir durumda yukarıdaki işlemi tersine yaparak geçmiş tarihe gitmeliyim.
2022 yılı Deflatör Endeksi = 2023 Yılı Deflatör Endeksi/[1+2023 Yılı Deflatör Üzerinden Enflasyon Oranı]
2021 yılı Deflatör Endeksi = 2022 Yılı Deflatör Endeksi/[1+2022 Yılı Deflatör Üzerinden Enflasyon Oranı]
.
.
.
1923 yılı Deflatör Endeksi = 1924 Yılı Deflatör Endeksi/[1+1924 Yılı Deflatör Üzerinden Enflasyon Oranı]
Bu işlemler ile 1923-2023 dönemi 2009=1 olacak şekilde deflatör serisini türetmiş oldum.
Yıllara Göre Nominal GSYH | 1923-2023 | TÜİK İle Uyumlu
3 | Türetmiş olduğumuz Reel GSYH serisi ile Deflatör Endeksi serimizi çarparsak 1923-2023 dönemine ilişkin TÜİK ile uyumlu nominal GSYH serisini türetmiş oluruz.
Yıllara Göre Dolar Bazında GSYH | 1923-2023 | TÜİK İle Uyumlu
4 | TÜİK’in ham verileri üzerinden nominal GSYH’yi, dolar cinsinden nominal GSYH’ye bölersek, GSYH’yi dolara dönüştürülürken kullanılan dolar kurunu buluruz. Türettiğimiz nominal GSYH’yi TÜİK’in bu zımni kuruna bölersek dolar bazında GSYH’ye (nominal) ulaşırız.
1923 yılı için TÜİK’in ham verisinde GSYH 577 milyon dolar iken, yukarıda türettiğimiz seride 1,15 milyar dolardır.
YILLARA GÖRE DOLAR BAZINDA KİŞİ BAŞINA GSYH | TL BAZINDA KİŞİ BAŞINA GSYH
Kişi Başına GSYH yıl ortası nüfustan hareketle hesaplanmıştır. 2023 yılı için yıl ortası nüfusu aşağıda gösterildiği şekilde hesaplayabiliriz.
[2022 yılı yıl sonu nüfusu]+[2023 yılı yıl sonu nüfusu]/2= 2023 yılı yıl ortası nüfusu
Yıllara Göre Dolar Bazında Kişi Başına GSYH | TL Bazında Kişi Başına GSYH
Dolar Bazında GSYH serisini nüfusa bölersek, Dolar Bazında Kişi Başına GSYH serisine ulaşırız.
1923 yılı için TÜİK’in ham verisinde kişi başına GSYH 45 dolar iken, yukarıda türettiğimiz seride 91 dolardır.